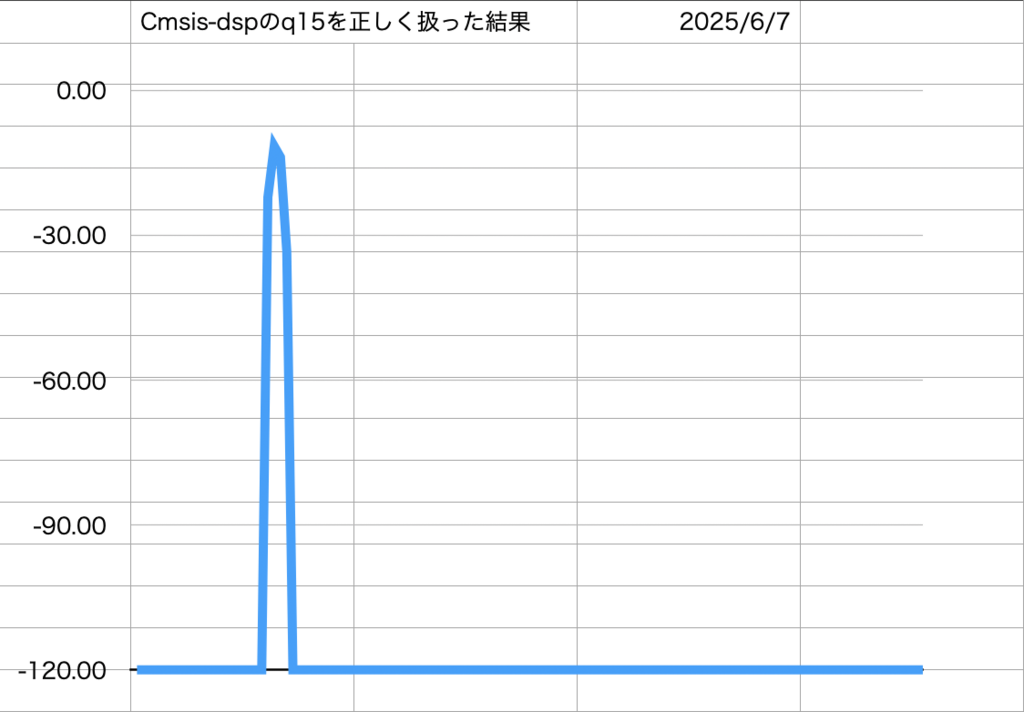
現実には窓関数を使うから、窓をかけるのと計算方法(元のソースは最後の出力配列作成時のq15の扱い方が変)だったので処理方法を見直して、対数表示でも違和感ないように見直し
<コードの波形部分以外の全部>
/* See https://m0agx.eu/practical-fft-on-microcontrollers-using-cmsis-dsp.html */
#include <math.h>
#include <ltstdio.h>
#include "arm_math.h"
#include "pico/stdlib.h"
#include "pico/time.h"
unsigned char __697hz_raw[] = {// データ部分は省略};
unsigned int __697hz_raw_len = 512;
#define FFT_SIZE 256
// バッファ宣言
q15_t input_signal[FFT_SIZE]; // 入力(実数信号)
q15_t fft_output[FFT_SIZE * 2]; // 出力(複素数 interleaved)
q15_t mag_squared[FFT_SIZE]; // パワースペクトル(Q13形式)
void perform_fft_and_power_spectrum(arm_rfft_instance_q15 *instance, q15_t *input, q15_t *output, q15_t *power_spectrum)
{
arm_rfft_q15(instance, input, output);
arm_cmplx_mag_squared_q15(output, power_spectrum, FFT_SIZE);
}
int main()
{
stdio_init_all();
sleep_ms(1000);
q15_t *input = (q15_t *)__697hz_raw;
q15_t windowed_input[FFT_SIZE];
float scaling_factor = 1.0f / 8192.0; // Q13 → float
float hann_correction = 1.0f / 0.5f; // ハニング窓で約0.5倍になる補正
// ハニング窓
for (int n = 0; n < FFT_SIZE; n++) { float hann = 0.5f * (1.0f - cosf(2.0f * M_PI * n / (FFT_SIZE - 1))); q15_t hann_q15 = (q15_t)(hann * 32767.0f); int32_t val = (int32_t)input[n] * hann_q15; windowed_input[n] = (q15_t)(val >> 15);
}
arm_rfft_instance_q15 fft_instance;
arm_status status = arm_rfft_init_q15(&fft_instance, FFT_SIZE, 0, 1);
printf("FFT init %d\n", status);
uint32_t start_time = time_us_32();
perform_fft_and_power_spectrum(&fft_instance, windowed_input, fft_output, mag_squared);
uint32_t end_time = time_us_32();
printf("Execution time: %.2f us per FFT\n", (float)(end_time - start_time));
for (uint32_t j = 0; j <= FFT_SIZE / 2; j++)
{
float mag = mag_squared[j] * scaling_factor * hann_correction;
float db = 10.0f * log10f(mag + 1e-12f); // 0対策のオフセット付き
printf("Bin %3u: %.2f dB\n", j, db);
}
printf("\n");
__BKPT(1);
}
<結果>
窓はHanningが適切っぽいし、フレーム数も256で簡易表示なら速度的にも速いから良さそうだ
ADCはノイジーだけど内蔵の12 bitsでやってみるのがPoCには適切だろうと思う
admin