FFTの実行速度をbumpy FFTとRustのクレートである、
https://docs.rs/rustfft/latest/rustfft/
と比較してみた
<条件>
Python numpy/rustfftでM1 Macとラズパイzero W
・実行条件
sampling_rate = 2000 # サンプリング周波数(Hz)
T = 1 / sampling_rate # サンプリング間隔
t = np.arange(0, 1.0, T) # 時間ベクトル
# 信号生成(50Hzと120Hzのサイン波を重ねたもの)
f1 = 100 # Hz
f2 = 300 # Hz
signal = np.sin(2*np.pi*f1*t) + 0.5*np.sin(2*np.pi*f2*t)
<実行速度>
M1 MacBook Air: np.fft.fft: 0.000027 [sec]
ラズパイzero W: np.fft.fft: 0.001830 [sec] ふーむ、およそ60倍ぐらい違うか、想定範囲だけど
<rustfftで実行>
・実行条件
const N: usize = 1024; // FFT size
const SAMPLE_RATE: f32 = 100.0; // sampling rate
const INPUT_FREQ: f32 = 20.0; // input frequency
どちらもreleaseモードでコンパイル、ほぼ条件は同じでnumpyfftとrustfftは同等の実行速度で、Cで記述されているだろうnumpyだからある意味当然の結果です
M1 MacBook Air
Elapsed time: 31.583µs
(参考値:debugモードでコンパイル)
Elapsed time: 1.878708ms
ラズパイzero W
$ ./fft
Elapsed time: 1.957008ms・Rustのコード
fftは複素数で計算していますが、データはre部分だけ作成、結果は複素数になるので絶対値を求めてVecに格納、このクレートは入力データのVecに計算結果が格納されるという変則的なクレートのように思う
// Computes a forward FFT
//
use plotters::prelude::*;
use rustfft::{FftPlanner, num_complex::Complex};
use std::f32::consts::PI;
use std::time::Instant;
const N: usize = 1024; // FFT size
const SAMPLE_RATE: f32 = 100.0; // sampling rate
const INPUT_FREQ: f32 = 20.0; // input frequency
// prepare target data
fn complex_vector(length: usize, dt: f32, frequency: f32) -> Vec<Complex<f32>> {
(0..length)
.map(|i| {
let t = i as f32 * dt;
let phase = frequency * 2.0 * PI * t;
let phase2 = 3.0 * frequency * 2.0 * PI * t;
Complex::new(phase.sin() + phase2.sin(), 0.0)
})
.collect()
}
fn draw(x: Vec<usize>, y: Vec<f32>) -> Result<(), Box<dyn std::error::error="">> {
let image_width = 1080;
let image_height = 720;
let root = BitMapBackend::new("plot.png", (image_width, image_height)).into_drawing_area();
root.fill(&WHITE)?;
// https://qiita.com/lo48576/items/343ca40a03c3b86b67cb
let (y_min, y_max) = y
.iter()
.fold((0.0 / 0.0, 0.0 / 0.0), |(m, n), v| (v.min(m), v.max(n)));
let caption = "DFT result";
let font = ("sans-serif", 20);
let mut chart = ChartBuilder::on(&root)
.caption(caption, font.into_font())
.margin(10)
.x_label_area_size(16)
.y_label_area_size(42)
.build_cartesian_2d(
*x.first().unwrap()..*x.last().unwrap(),
y_min..y_max,
)?;
chart.configure_mesh().draw()?;
let line_series = LineSeries::new(x.iter().zip(y.iter()).map(|(x, y)| (*x, *y)), &RED);
chart.draw_series(line_series)?;
Ok(())
}
fn main() {
// fft data preparation
let sr = 1.0/SAMPLE_RATE;
let mut buffer = complex_vector(N, sr, INPUT_FREQ);
// fft mode setting
let mut planner = FftPlanner::new();
let fft = planner.plan_fft_forward(N);
let start_time = Instant::now();
// fft exec
fft.process(&mut buffer);
let end_time = Instant::now();
println!("Elapsed time: {:?}", end_time.duration_since(start_time));
// absolute value calc
let y: Vec<f32> = buffer.iter().map(|z| z.norm()).collect();
// drwa graph
let n = N;
let x: Vec<usize> = (1..=n).collect();
let _ = draw(x, y);
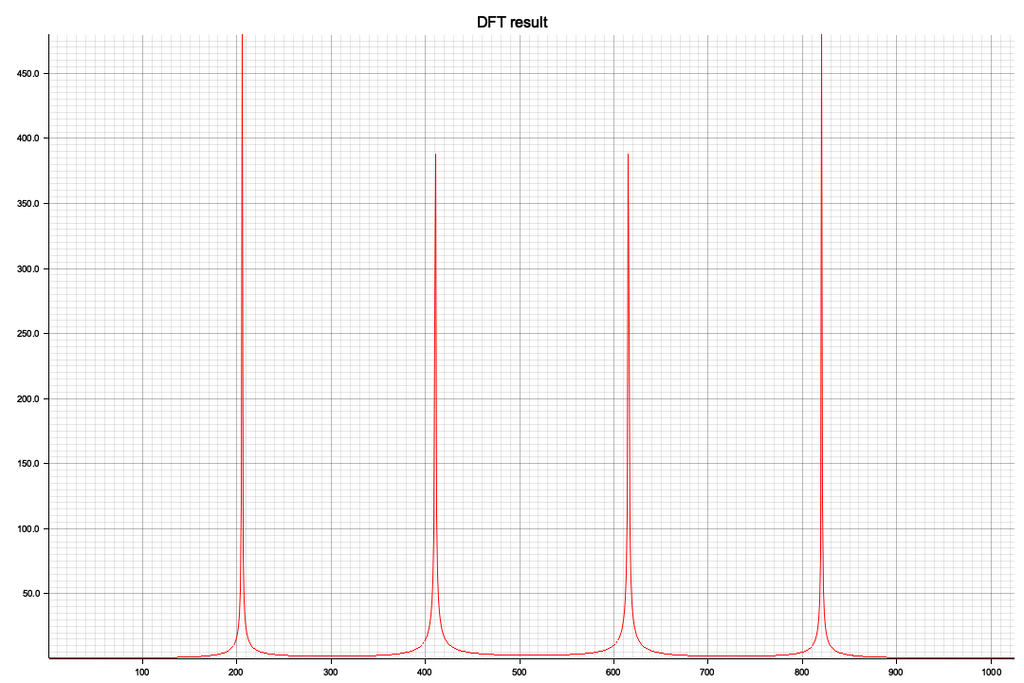
}ビジュアル化した結果、x軸の512を境に対称形になっています、レベル(ピーク値)が違うのは今のところ謎
admin