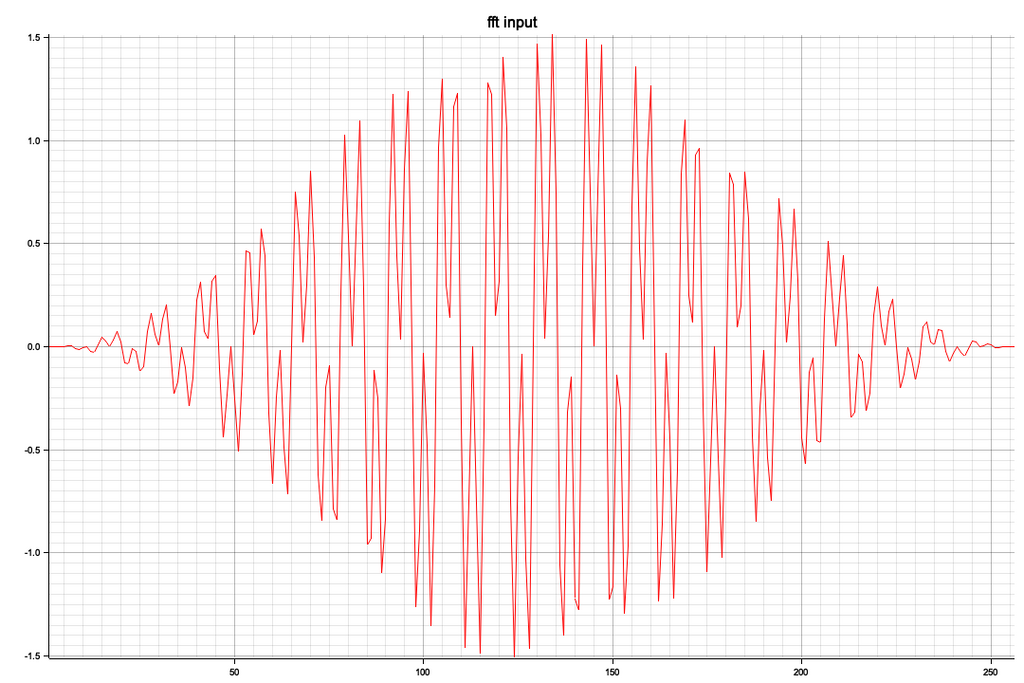
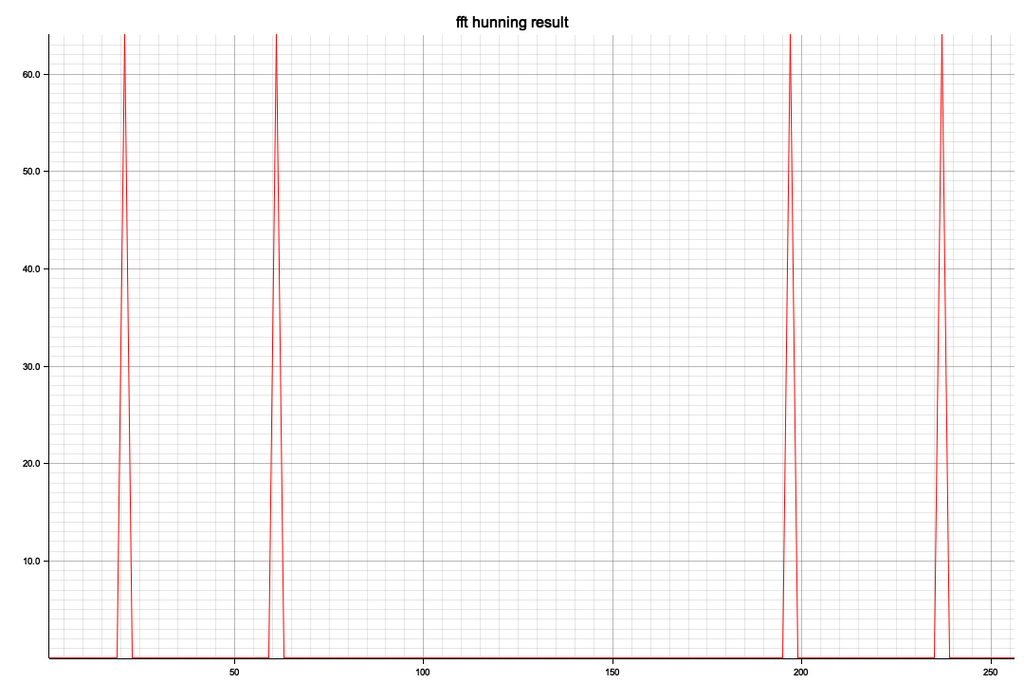
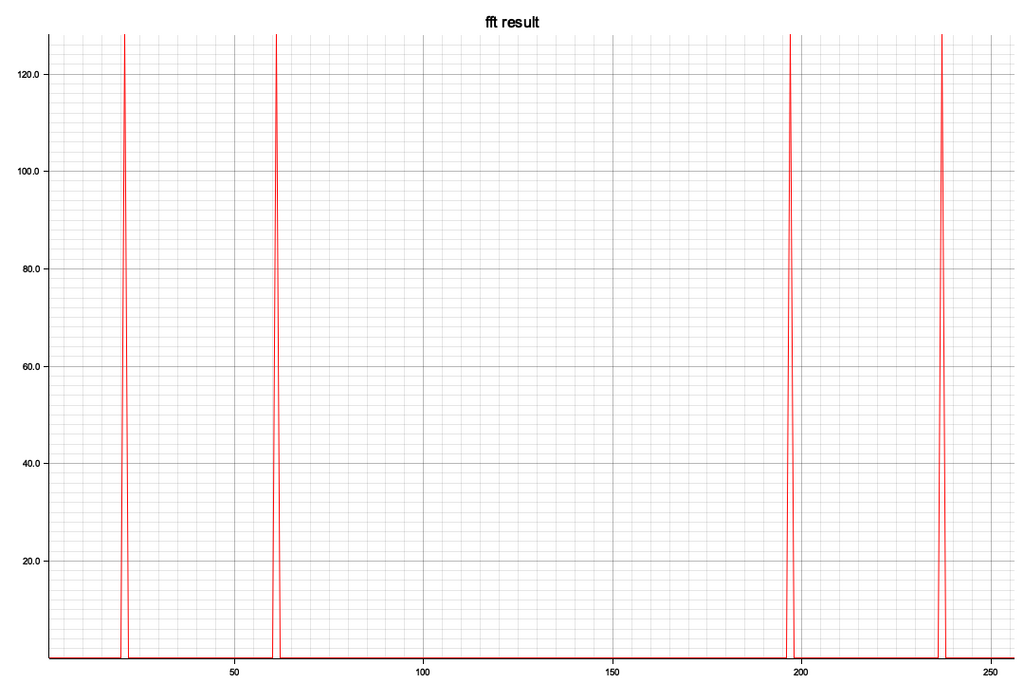
実際のFFTでは無限に継続する波形というのはないので、実用的なアプリケーションでは信号の切り出しが必要です
ところでrustfftには窓機能のメソッドはないので、個別に実装が必要ですが、一番ポピュラーと思うhanning窓を適用してみました
hanning窓は(1-cos(x))/2で表現されますが、前回の正弦波の合成波形にこの窓を適用します
<窓適用後の入力波形>
<FFTの結果>
比較用の窓処理なしのスペクトル
窓をかけるとピークレベルはほぼ半分になります(対称波形のエンベロープの面積から)、また多少スペクトルの根元が広がっています、予測ではもっと広がると思ってた
P.S. 2024/10/28
スペクトルの分散の考え方は、このケースでは正弦波を窓関数でAM変調していると捉えれば、キャリア周波数の両サイドに山がいくつか見えるはずで、周波数分解能が足りないからダンゴになって見えているだけです
<コード>
正弦波の合成のところで窓処理も同時に行ってます
use plotters::prelude::*;
use rustfft::{num_complex::Complex, FftPlanner};
use std::f32::consts::PI;
use std::time::Instant;
const N: usize = 256; // FFT size
const SAMPLE_RATE: f32 = 256.0; // sampling rate
const INPUT_FREQ: f32 = 20.0; // input frequency
fn complex_vector_with_hanning(length: usize, dt: f32, frequency: f32) -> Vec<Complex<f32>> {
(0..length)
.map(|i| {
let t = i as f32 * dt;
let phase = frequency * 2.0 * PI * t;
let phase2 = 3.0 * frequency * 2.0 * PI * t;
Complex::new(
(f32::sin(phase) + f32::sin(phase2)) * 0.5 * (1.0 - f32::cos(2.0 * PI * t)),
0.0,
)
})
.collect()
}
fn re_vector(complex_numbers: Vec<Complex<f32>>) -> Vec<f32> {
complex_numbers.iter().map(|z| z.re).collect()
}
fn draw(
x: Vec<usize>,
y: Vec<f32>,
f_name: &str,
cap: &str,
) -> Result<(), Box<dyn std::error::Error>> {
let image_width = 1080;
let image_height = 720;
let root = BitMapBackend::new(f_name, (image_width, image_height)).into_drawing_area();
root.fill(&WHITE)?;
// https://qiita.com/lo48576/items/343ca40a03c3b86b67cb
let (y_min, y_max) = y
.iter()
.fold((0.0 / 0.0, 0.0 / 0.0), |(m, n), v| (v.min(m), v.max(n)));
let caption = cap;
let font = (“sans-serif”, 20);
let mut chart = ChartBuilder::on(&root)
.caption(caption, font.into_font())
.margin(10)
.x_label_area_size(16)
.y_label_area_size(42)
.build_cartesian_2d(*x.first().unwrap()..*x.last().unwrap(), y_min..y_max)?;
chart.configure_mesh().draw()?;
let line_series = LineSeries::new(x.iter().zip(y.iter()).map(|(x, y)| (*x, *y)), &RED);
chart.draw_series(line_series)?;
Ok(())
}
fn main() {
// fft data preparation with window
let sr = 1.0 / SAMPLE_RATE;
let mut buffer = complex_vector_with_hanning(N, sr, INPUT_FREQ);
// draw input signal
let buf_re = re_vector(buffer.clone());
let n = N;
let f_input = “plot_input.png”;
let cap = “fft input”;
let x: Vec<usize> = (1..=n).collect();
let _ = draw(x, buf_re, &f_input, &cap);
// fft mode setting
let mut planner: FftPlanner<f32> = FftPlanner::new();
let fft = planner.plan_fft_forward(N);
let start_time = Instant::now();
// fft exec
fft.process(&mut buffer);
let end_time = Instant::now();
println!(“Elapsed time for FFT: {:?}”, end_time.duration_since(start_time));
// absolute value calc
let y: Vec<f32> = buffer.iter().map(|z| z.norm()).collect();
// draw fft graph output
let n = N;
let file_fft = “plot_fft_hanning.png”;
let cap = “fft hanning result”;
let x: Vec<usize> = (1..=n).collect();
let _ = draw(x, y, &file_fft, &cap);
}
admin